二叉树
二叉树的遍历:
前序遍历:根左右;
中序遍历:左根右;
后序遍历:左右根;
结点定义
1
2
3
4
5
6
7
8
9
10
| struct TreeNode
{
char val;
TreeNode *lchild;
TreeNode *rchild;
TreeNode(char val){
this->val = val;
this->lchild = this->rchild = NULL;
}
};
|
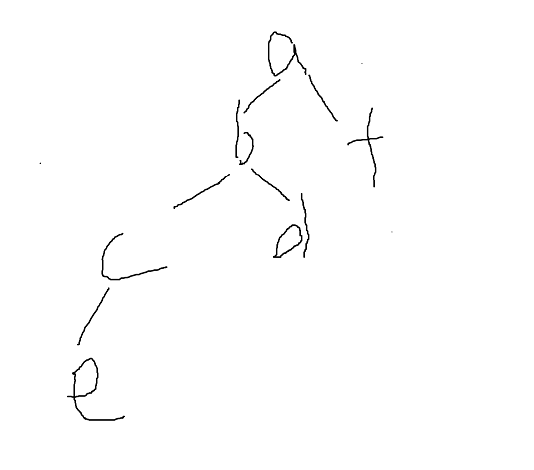
前序遍历
递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
void PreOrderTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
else
{
cout<<root->val<<",";
PreOrderTraversal(root->lchild);
PreOrderTraversal(root->rchild);
}
}
|
输出结果:
a,b,c,e,d,f,
利用栈实现
首先将root入栈,创建一个临时结点指向栈顶元素,依次判断其右结点、左节点 是否为 NULL,不是的话则入栈,只要栈内的元素不为空 每次while循环就可以弹出一个元素,做到遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| void PreOrder_staTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
else
{
stack<TreeNode*> stk;
stk.push(root);
while (!stk.empty())
{
TreeNode *pnode = stk.top();
stk.pop();
cout<<pnode->val<<endl;
if (pnode->rchild != NULL)
{
stk.push(pnode->rchild);
}
if (pnode->lchild != NULL)
{
stk.push(pnode->lchild);
}
}
}
}
|
输出结果一致。
利用morris实现
morris原理:
把当前的结点记作pnode,
如果pnode的左子节点为NULL,则 让pnode指向pnode的右子节点(pnode=p->rchild);
如果pnode的左子节点不为NULL,则找到其左子树的最右结点,记为mostright;
(1). 如果mostright的右子节点指向为NULL,则让mostright的右子节点指向pnode,
并且让pnode左移,即pnode = pnode->lchild;
(2). 如果mostright的右子节点指向pnode,则让mostright的右字节带你指向为NULL,
并且让pnode右移,即pnode = pnode->rchild;
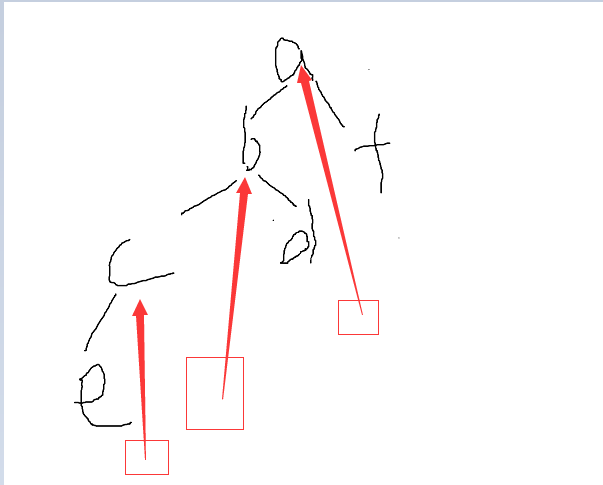
分析过程原理:
按照上述的原理
pnode指向a,mostright为d,d的右子节点为NULL,则d的右子节点指向pnode,即指向a,pnode再左移,
pnode指向b,mostright为c,c的右子节点为NULL,则c的右子节点指向pnode,即指向b,
pnode左移,
pnode指向c,mostright为e,e的右子节点为NULL,则e的有子结点指向pnode,即指向c,
pnode左移,
pnode指向e,p的左节点为空,所以pnode右移,即pnode = pnode->rchild,而e的右子节点指向了c,所以pnode此时又指向回到了c
pnode指向c,mostright为e,mostright的右子节点指向不为NULL,指向c,所以pnode右移,
在第2步当中c的右子节点指向了b,所以pnode回到b,
pnode指向b,mostright为c,mostright的右子节点指向不为NULL,指向b,所以pnode右移,
pnode指向d,d的左子树为NULL,所以pnode右移,在第一步,d的右子树指向a,所以pnode回到a
pnode指向a,mostright为d,mostright的右子树不为NULL,所以pnode右移,指向f
pnode指向f…………
……
……
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| void morris(TreeNode *root)
{
if (root == NULL)
{
return ;
}
else
{
TreeNode *pnode = root;
while ( pnode != NULL)
{
if (pnode->lchild == NULL)
{
cout<<pnode->val<<endl;
pnode = pnode->rchild;
}
else
{
TreeNode *MostRight = pnode->lchild;
while (MostRight->rchild != NULL && MostRight->rchild != pnode)
{
MostRight = MostRight->rchild;
}
if (MostRight->rchild == NULL)
{
MostRight->rchild = pnode;
cout<<pnode->val<<endl;
pnode = pnode->lchild;
}
else if (MostRight->rchild == pnode)
{
MostRight->rchild == NULL;
pnode = pnode->rchild;
}
}
}
}
}
|
输出结果一致。
中序遍历
递归实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void InOrderTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
else
{
InOrderTraversal(root->lchild);
cout<<root->val<<" ";
InOrderTraversal(root->rchild);
}
}
|
输出结果:
e c b d a f

使用辅助栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void InOrder_staTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
stack<TreeNode*> nodeStack;
TreeNode* pnode = root;
while (pnode != NULL || !nodeStack.empty())
{
if (pnode != NULL)
{
nodeStack.push(pnode);
pnode = pnode->lchild;
}
else
{
pnode = nodeStack.top();
nodeStack.pop();
cout<<pnode->val<<" ";
pnode = pnode->rchild;
}
}
}
|
输出结果一致;
morris算法
原理一致,只是在输出位置改变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| void InMorris(TreeNode *root)
{
if (root == NULL)
{
return ;
}
TreeNode* pnode = root;
while (pnode != NULL)
{
if (pnode->lchild == NULL)
{
cout<<pnode->val<<" ";
pnode = pnode->rchild;
}
else
{
TreeNode *MostRight = pnode->lchild;
while (MostRight->rchild != NULL && MostRight->rchild != pnode)
{
MostRight = MostRight->rchild;
}
if (MostRight->rchild == NULL)
{
MostRight->rchild = pnode;
pnode= pnode->lchild;
}
else
{
MostRight->rchild = NULL;
cout<<pnode->val<<" ";
pnode = pnode->rchild;
}
}
}
}
|
后序遍历
递归实现:
1
2
3
4
5
6
7
8
9
10
| void PostOrderTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
PostOrderTraversal(root->lchild);
PostOrderTraversal(root->rchild);
cout<<root->val<<" ";
}
|

使用辅助栈
这里可用到两个辅助栈,一个用来记录结点入栈的顺序,最后再出栈做到遍历的效果;另一个栈用来暂存结点。
*难点在于,当指针访问到该结点时,发现该节点为空,然后会回指到父节点,此时就不清楚是第一次从左子树回到父节点还是从右子树回到父节点, 在右子树回到父节点时,我们应当对当前父节点的值进行输出;
可以在每个结点上存一个标志符,当从左节点回到父节点的时候,更改标志符,
在右节点回到父节点时,即可根据标志符来进行输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| void PostOrder_staTraversal(TreeNode *root)
{
if (root == NULL)
{
return ;
}
stack<TreeNode *> NodeStack;
stack<TreeNode *> PutStack;
TreeNode *pnode = root;
while (pnode || !NodeStack.empty())
{
if (pnode)
{
NodeStack.push(pnode);
PutStack.push(pnode);
pnode = pnode->rchild;
}
else
{
pnode = NodeStack.top()->lchild;
NodeStack.pop();
}
}
while (!PutStack.empty())
{
cout<<PutStack.top()->val<<" ";
PutStack.pop();
}
}
|
输出结果:
e c d b f a




