快速排序

基本简介

快速排序（Quicksort）是对冒泡排序的一种改进。由C. A. R. Hoare在1962年提出。

它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

算法描述

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它左边，所有比它大的数都放到它右边，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

3）从j开始向前搜索，即由后开始向前搜索(j–)，找到第一个小于key的值A[j]，将A[j]和A[i]的值交换；

4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]的值交换；

5）重复第3、4步，直到i==j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

排序演示

假设一开始序列{xi}是：5，3，7，6，4，1，0，2，9，10，8。

此时，ref=5，i=1，j=11，从后往前找，第一个比5小的数是x8=2，因此序列为：2，3，7，6，4，1，0，5，9，10，8。

此时i=1，j=8，从前往后找，第一个比5大的数是x3=7，因此序列为：2，3，5，6，4，1，0，7，9，10，8。

此时，i=3，j=8，从第8位往前找，第一个比5小的数是x7=0，因此：2，3，0，6，4，1，5，7，9，10，8。

此时，i=3，j=7，从第3位往后找，第一个比5大的数是x4=6，因此：2，3，0，5，4，1，6，7，9，10，8。

此时，i=4，j=7，从第7位往前找，第一个比5小的数是x6=1，因此：2，3，0，1，4，5，6，7，9，10，8。

此时，i=4，j=6，从第4位往后找，直到第6位才有比5大的数，这时，i=j=6，ref成为一条分界线，它之前的数都比它小，之后的数都比它大，对于前后两部分数，可以采用同样的方法来排序。

动图演示

说明 ：原理演示均来自百度百科。

那么基于c语言实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <stdio.h>
#include <stdlib.h>

int partition (int a[],int left,int right);
//  定义一个函数来对一个数进行归位
/* 我定义归位的意思就是 把一个数放到中间某个位置，他的左边都是比他小的数，他的右边都是比他大的数；
然后对左右两边进行递归归位.
*/
void quick_sort(int a[],int left,int right);

int main (){
    int a[] = {5,8,6,4,3,9,2,7,1};
    int right=sizeof(a)/sizeof(a[0]);
    for(int i=0;i<right;i++){
        printf("%d ",a[i]);
    }
    printf("\n");
    // 这里做遍历为了调试时便于比较
    quick_sort(a,0,right-1);
    for(int i=0;i<right;i++){
        printf("%d ",a[i]);
    }
    system("pause");
    return 0;
}

int partition (int a[],int left,int right){
    int len = right;
    int temp = a[left];  // 用temp来暂时储存要归位的那个数
    while (left<right){
        while (left < right && a[right]>= temp){
            right--;
        }
        a[left] = a[right];
        //  从右边找一个小于归位的那个数的值放入最开始归位那个数的位置
        for (int i = 0;i<=len;i++){
            printf("%d ",a[i]);
        }
        printf("\n");
        // 对每次右边找数做一次输出
        while (left < right && a[left]<= temp){
            left++;
        }
        a[right] = a[left];
        //  从左边找一个大于归位那个数的值放入右边空出来的位置
        //（这个位置是上面找的那个小于归位那个数的位置）
        for (int i = 0;i<=len;i++){
            printf("%d ",a[i]);
        }
        printf("\n");
		// 对每次左边找数做一次输出
    }
    a[left] = temp;  // 最后把归位那个数放在 left或者right的位置
    return left; // 这里返回left，right都可 以为循环结束时left等于right
}


void quick_sort (int a[],int left,int right){
    if (left < right ){  // 满足数组至少两位
        int mid = partition(a,left,right); /* 定义的mid 但它不一定就是在正中间的位置，
        而是中间的某个位置 */
        quick_sort(a,left,mid-1);//对归位那个数的左边进行递归
        quick_sort(a,mid+1,right); // 对归位那个数的右边进行递归
    }
}

输出结果

5 8 6 4 3 9 2 7 1
1 8 6 4 3 9 2 7 1
1 8 6 4 3 9 2 7 8
1 2 6 4 3 9 2 7 8
1 2 6 4 3 9 6 7 8
1 2 3 4 3 9 6 7 8
1 2 3 4 3 9 6 7 8
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4 5 8 6 7 8
1 2 3 4 5 8 6 7 8
1 2 3 4 5 7 6 7
1 2 3 4 5 7 6 7
1 2 3 4 5 6 6
1 2 3 4 5 6 6
1 2 3 4 5 6 7 8 9

分析

时间复杂度：

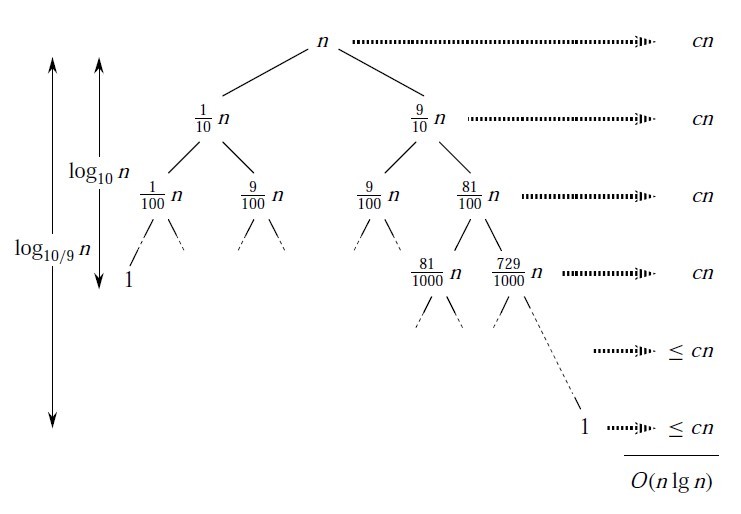
我们发现第一次归位，是将整个数组分成了两份，然后再分别对右边和左边的数重复这个操作；那么他不断分成两份的这个过程便是logn；意思就是第一次需要进行一次归位操作；第二次需要进行两次归位操作;第三次需要进行4次归位，第四次需要进行8次归位……依次下来就是logn次归位（第一次和第二次以及之后的每一次归位操作的时间复杂度都是一次归位的时间复杂度，我们记一次归位的时间复杂度为O（x），那么2O（x）和8O（x）本质一样），所以我们只需要分析归位操作的时间复杂度即可.

上述代码我们用partition表示归位操作；那么函数里面我们做的本质就是在一个while循环里从右边找一个填到左边，从左边找一个数填到右边，其实就是想到与一次一次比较然后换位的过程，所以时间复杂度应当就是O（n）。那么quick_sort的时间复杂度为O（nlogn）。

快速排序的最坏情况

当我们的一个数组为[9,8,7,6,5,4,3,2,1]时，那么对照算法他每次的归位的结果会是

1，8，7，6，5，4，3，2，9

1，8，7，6，5，4，3，2 再归位（此时9已经排好，在对9左右两边进行归位），

因为1右边的数都比他大所以又被写回来了

8，7，6，5，4，3，2 那么又回到最开始的情况

2，7，6，5，4，3

7，6，5，4，3

……….

所以一共时需要进行n次归位，那么此时最坏条件下的时间复杂度即为n².

其实我们要尽可能避免这种情况很简单，我们归位的那个数不是必须要从第0位开始，可以是随机数组中的任何一个位置，我们只需要把要归位的那个数与第0位的这个数调换位置，在执行quick_sort即可。

其实刁钻来讲，仍然存在一中最坏的条件，那就是我们每次随机的那个数刚好就是数组中的最大值，那么他的时间复杂度仍然还是O（n²），但这种几率小的可以忽略了。